Power

Let's revisit an example we discussed in the "Introduction to inferential statistics" module. (If you haven't done that module yet or if you don't remember this example, you may want to re-read it before continuing here.) Recall that in part 1 of that module we discussed a hypothetical study in which we measured the ages of PolyU graduate students and the ages of HKUST graduate students. Recall, also, that we imagined a fake situation where, in reality, the true difference between PolyU and HKUST graduate students is 2 years (the average for all PolyU students was 27, and the average for all HKUST students was 25). Remember that I gave you an Excel sheet with the data from the entire population of PolyU and HKUST students (remember these are just made-up data), and I asked you to randomly choose 10 PolyU students and 10 HKUST students and and see if you got the "correct" result (with PolyU students being older than HKUST students). Finally, remember that I said I used a computer program to repeat that procedure (selecting 10 random PolyU students and 10 random HKUST students) 500 times, and 18% of the random samples I selected had a "wrong" answer (with the sample of PolyU students being younger than the sample of HKUST students).

Specifically, if we know (or assume) certain properties of the population (e.g., in that example, I created a fake population in which the 500 PolyU students have an average age of 27 years [standard deviation 5.8 years] and the 500 HKUST students have an average age of 25 years [standard deviation 5.4 years]), and we know certain properties of the study (the fact that we pick 10 random PolyU students and 10 random HKUST students), we can figure out what percentage of the time our experiment will discover the "correct" result. In this example, the experiment will get the right result (PolyU older than HKUST) 82% of the time. We say the experiment has 82% power.

Recall that in that same activity, we also repeated this procedure with 30 PolyU students and 30 HKUST students, and I reported that when I did that 500 times (again, using a computer program), I got the right results 93% of the time instead of 82% of the time. In other words, the experiment with more people (30 per school, instead of 10 per school) had higher power: 93%.

If there is a difference in the population (like there was in our PolyU-HKUST example, since it's using a fake population of data that I intentionally created to have a difference), then there are lots of things that can influence how likely we are to detect it (i.e., there are lots of things that can influence our study's power). One, as we saw above, is the number of observations (e.g., people) in the sample: all else being equal, a study with more people in the sample will have higher power. Another thing that affects power is the effect size: if the difference between PolyU and HKUST students was 40 years instead of just 2 years, it would be much easier to detect, and thus we would have higher power. (Recall that, in the "Introduction to inferential statistics" module, we discussed how the formula for the t statistic gracefully summarizes three of the main things you can do to maximize the power in a study.)

In a simple experiment, these three things—sample size, effect size, and power—are deterministic (by which I mean, if you know two of them, you can figure out the third). For more complicated experiments there will be more factors to consider, and we'll discuss that later in this activity. Also note that I'm talking about standardized effect size here, such as Cohen's d: a 2-year difference between two groups with very small standard deviations may be a "bigger" difference than a 20-year difference between two groups with very large standard deviations, and Cohen's d captures that (since the former difference will be many standard deviations [and thus high d] and the latter difference will be few standard deviations or even less than a standard deviation [and thus low d]). In other words, if you want to design an experiment with 80% power to detect an effect of a certain size, you can calculate how many participants you need in your sample; or, if you plan to do an experiment with 30 participants, you can calculate what's the smallest effect size that you have 80% power to detect; or, if you plan to do an experiment with 30 participants and you expect the effect size is likely to be d=0.5, you can calculate what your power is to detect that effect. These kinds of analysis are all called power analysis.

Note that power analysis should only be done before doing a study; it's something you do when planning your research. Power analysis done after you've already seen the results (sometimes called post-hoc power analysis or observed power) is pointless; see Hoenig & Heisey (2001) for further discussion.

Complete the exercises below to learn more details about power analysis as it applies to linguistic research.

Because power analysis is a part of study planning, it will often be the case that you don't have a specific sample size in mind; instead, you might want to try power analysis on a lot of different sample sizes, in order to see which sample size will give you enough power to conduct the study. People's goal is often to design a study with at least 80% power to detect the effect they're interested in. Thus, people will often make a power curve, showing the calculated power for various sample sizes, to see which sample size gets 80% power or more. For example, maybe your power calculations show that if you do an experiment with 10 participants in each group you'll only have about 25% power to detect the effect size you're interested in, with 20 participants per group you'll have about 45% power, with 30 per group you'll have 62% power, with 40 you'll have 75% power, and at 45 participants per group you'll finally reach 80% power. Thus, you might then plan to do your study with 45 participants in each group (90 total).

See this blog post for a similar point as what I just described above.

You can make power curves like this with this useful web app. This works for simple research designs, e.g. in which one person contributes one data point; we will discuss more complicated designs in the next exercise. When you open this app and make a power curve, the bottom left graph will show the kind of power curve I was discussing above; the other graphs show different useful curves (remember that power analysis can be used to calculate different things, and thus we can show different combinations of things in these curves.)

Play with the power curve app to see how different sample sizes and different effect sizes influence power.

Think about the situation I described at the beginning of this question (a study where 10 participants per group will yield 25% power, 20 participants per group will yield about 45% power, etc.). How big does the effect size (Cohen's d) need to be to yield this particular power curve?

The example we discussed previously was of a very simple research design, in which you compare two groups directly, and each participant in each group just contributes one number to the dataset. Cases like this are simple, and there are simple math formulae or simple online tools ("power calculators") to deal with them. In most linguistics research, however, study designs are more complicated.

For example, in many studies, there is not just one piece of data per participant. Maybe a participant responds to many things (many questions in a test, or many trials in a psycholinguistic or phonetic experiment, etc.), and the score we get for that participant later is an average across those. Therefore, to design a study like that, we have to decide not just how many participants to recruit in our experiment, but how many trials/items/questions each participant should see. Thus, we might make more complicated power curves. Here's an example from a power analysis I did for one of my studies

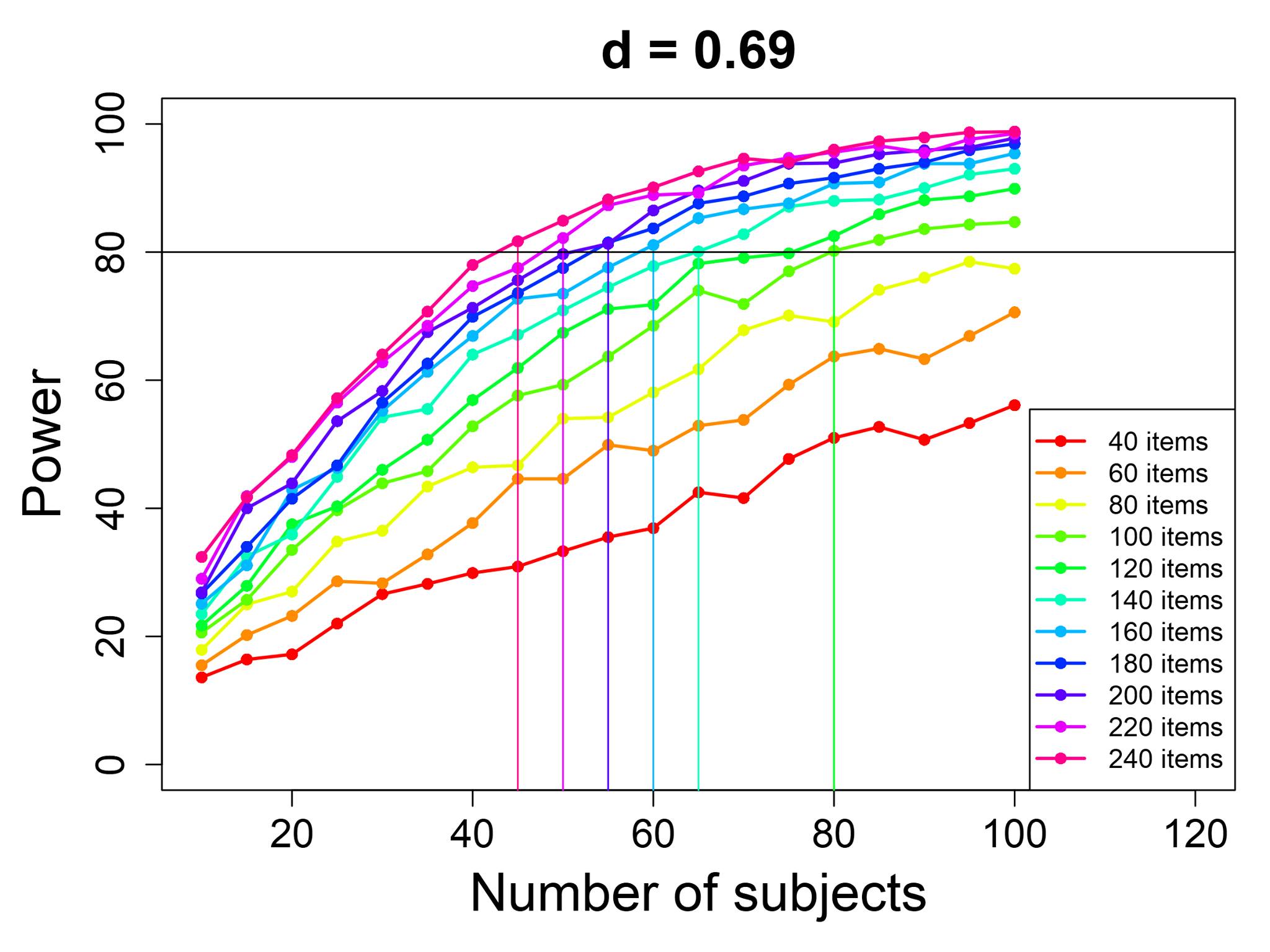
A series of power curves showing calculated power for different combinations of participants and items.

I made this when I was planning an ERP experiment (see the "Electrophysiology" module to learn more). In this kind of study, we let people be exposed to many linguistic stimuli (usually sentences, words, sounds, or something like that), and then we average together their brain responses to the stimuli. Thus, I had to decide both how many participants to get, and how many words ("items") to play to each participant. I expected, based on reviewing previous experiments on similar topics, that the effect size in my study might be close to d=0.69. Thus, I made these curves to help make my decision; the vertical lines show, for any given number of items, what's the smallest number of participants that would give me at least 80 power. (These values were calculated from another web-based power calculator, specifically designed for ERP data.)

I can see, for example, that if I make an experiment with 240 words, then I will need around 45 participants to reach 80% power; however, it might be hard to find enough appropriate words to use for this study! On the other hand, I could make an experiment with only 120 words, and still get 80% power... but then I would need to find 80 people, instead of 45, to join my experiment. So there are power tradeoffs to be made.

You can also use these kinds of power curves to see what your maximum ideal number of participants or items should be. For example, if the number of participants is above 60, then the lines for 200 items, 220 items, and 240 items are all pretty much together; in other words, if I have 200 items and 60 participants, then there's not much benefit to adding more items! Likewise, if I have 240 items and 70 participants, then the line gets pretty flat, meaning that there's not much benefit to adding more participants.

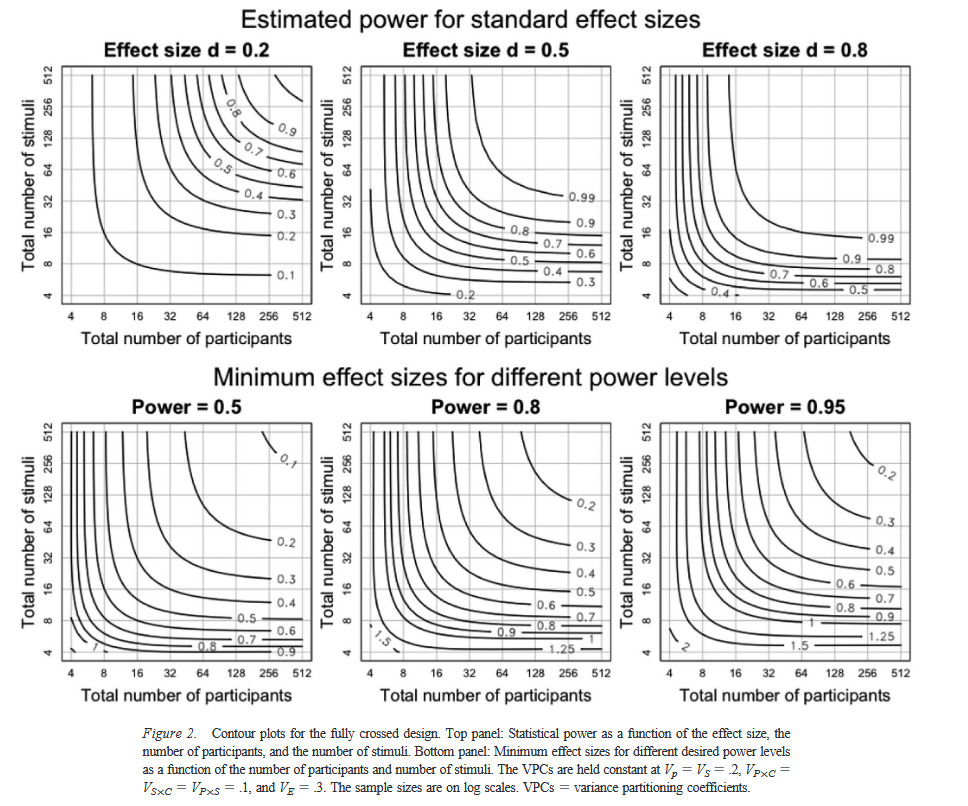
For realistic experiment designs, there start to be a lot of different things that can influence power (the EEG example above was already pretty simplified), and it can become very complicated to calculate power; Westfall et al. (2014) discuss this issue in much more detail. For now, just consider the set of power curves shown below from their paper. This is showing the same sort of thing as my above example, just in a different format (the y-axis represents number of items now, instead of power, and the different lines represent different power levels). Based on these graphs, if you are doing an experiment where you expect an effect size of d=0.5, how many participants and items would you plan to have in your experiment?

Figure 2 of Westfall et al. 2014 (link in main text) showing a series of power curves for different effect sizes, participant sample sizes, and item sample sizes.

In reality, doing accurate power analysis is often impossible. As you've seen from the previous question, it needs many kinds of information that you might not know, such as the expected effect size; if you look in detail at the Westfall et al. (2014) paper or my ERP power calculator, you see that it also needs you to fill in a lot of numbers such as the within-participant variance and complicated stuff like that. Expected effect size is hard to know (your research hypothesis is probably something like "I expect this will be bigger than that", rather than "I expect this will be 0.73 standard deviations bigger than that"!), but at least you might have a reasonable feeling about it when you look at other research (at least you might know if this effect tends to be big or small). However, things like the amount of within-participants variance is something that it's hard to have intuition about. Therefore, often the only way to do a good power analysis is to have a previous dataset (e.g., from an experiment you did before, or from someone else's experiment if they make their data available—for example, many psycholinguistic datasets are available at this repository). You can't just use pilot data (e.g., running a mini-experiment with two or three people) to estimate these values, because data from a small number of people won't give an accurate estimate; you really need to have a whole dataset.

So, what do you do when you don't have a previous dataset? What if you're doing someone no one else has done before?

In such a situation, you might not be able to calculate power, but you can at least do things that you know will increase power. For example, in this paper I could not do power analysis but I just listed many things that we did in the study to increase power. Some things that increase power:

Having more participants. If two studies are equal in every way except the number of participants, then the study with more participants will have more power. Most studies in our field are underpowered, especially studies done more than a few years ago. Thus, as a rule of thumb, you can look at how many participants most previous studies used, and just double or triple that.
The above also applies to number of items, stimuli, or anything else like that.
The other thing that makes power bigger is having a bigger effect, and/or less variance around that effect. So you can make the effect as big as possible by designing your study well—for example, making sure you design the study to elicit the effect strongly. You can also reduce the variation of the effect by keeping your study well-controlled—for example, testing all your participants under the same conditions (and using within-participant designs, rather than between-participants designs, as much as possible). (Of course, there may be trade-offs here: for example, if you control the participants very carefully then it might be hard to get a large number of participants, or if you get a large number of participants it might be hard to control their characteristics very well.) Finally, appropriate statistical methods can help you have a bigger effect or have less variance around your effect; for example, using regression to parcel out extra sources of variation (see the "Regression" model for details) can help you identify your effect more precisely, and thus have more power.

Think about your own research. What can you do to maximize your statistical power in a study you are planning?

After you finish this activity, do the "Confidence intervals" activity if you have not already. If you have finished both this and Power, then you are done with the module (assuming all your work on this and the previous tasks has been satisfactory). However, you may still continue on to the advanced-level task for this module if you wish to complete this module at the advanced level (if you're aiming for a higher grade or if you are just particularly interested in this topic). Otherwise, you can return to the module homepage to review this module, or return to the class homepage to select a different module or assignment to do now.

Power (3 hours)